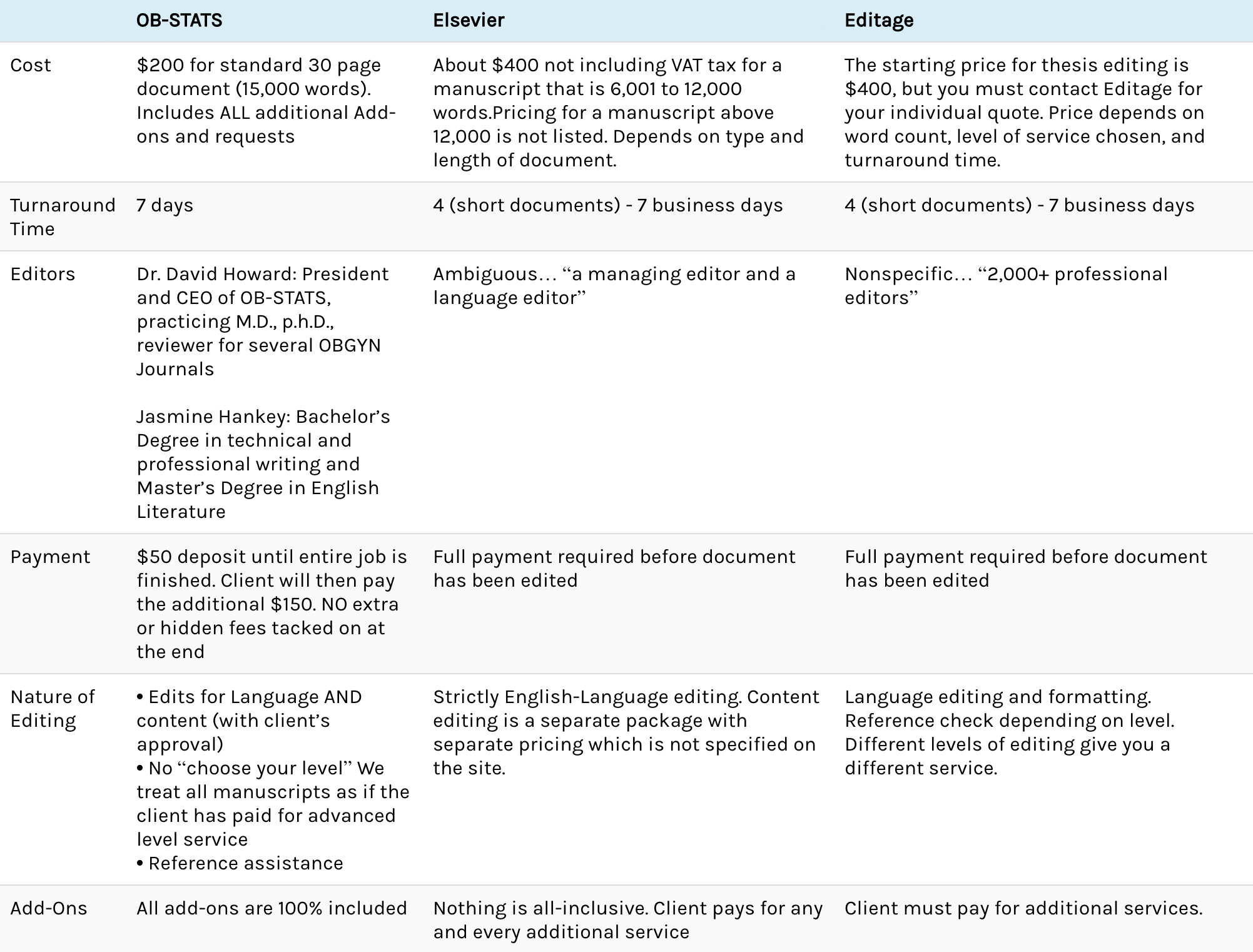
A statistical hypothesis test (also called a significance test) is a procedure designed to determine whether or not a null hypothesis provides a plausible explanation of the data.
There are two types of statistical hypotheses tests that we will discuss: the null hypothesis and the alternative hypothesis.
- Null Hypothesis: The null hypothesis is typically the hypothesis that the data being gathered is the result of random chance (one example being a model assuming no treatment effects).
- Alternative Hypothesis: The alternative hypothesis is typically the research hypothesis that the data being gathered is influenced by some non-random effect (one example being a model assuming that a treatment will, on average, work better than a control).
Test Statistics
Regarding the null hypothesis, a test statistic is a measure of the difference between the data observed and what is expected when the null hypothesis is true.
Commonly-used test statistics include:
- The t-statistic associated with the Student’s t-test
- The chi-square-statistic associated with the chi-square test
- The F statistic associated with the analysis of variance (ANOVA) test
When conducting a statistical hypothesis test, the following describes the steps used:
1. Formulate null and alternative hypotheses.
2. Calculate the test statistic. That test statistic is used to measure or represent the difference between the data collected and the data that would be expected if the null hypothesis were true.
3. Compare the calculated test statistic to a predetermined value to determine whether the null hypothesis will be rejected or not rejected. That predetermined value, in turn, is based on the amount of error tolerated in decision making.
4. If the calculated test statistic is greater than the allowed value, then the null hypothesis is rejected. If the calculated test statistic is lesser, then the null hypothesis is not rejected.
Statistical Hypothesis Error Types
There are two types of error that are significant when hypothesis testing: Type 1 and Type 2.
• Type 1 Error: The probability of incorrectly rejecting the null hypothesis when it is true. There is no standard rule for the type 1 error. The type 1 error rate is set by the investigator based on the consequences of falsely rejecting the null hypothesis. The most level set for the type 1 error rate is 5%, or 0.05.
• Type 2 Error: The failure to reject a null hypothesis that is false. The type 2 error rate is based on the power of the study, which, in turn, is directly related to the sample size.
The following table describes the error types:
|
|
Truth About Population |
|
|
Decision Based on Sample |
H0 is true |
H0 is false |
|
Fail to reject H0 |
Correct Decision (probability = 1 – α) |
Type 2 Error: fail to reject H0 when it is false (probability = β) |
|
Reject H0 |
Type I Error: rejecting H0 when it is true (probability = α) |
Correct Decision (probability = 1 – β) |
Learn More With OB-STATS
“How To Do A Research Project” was developed by Dr. David Howard. Having earned both a phD and MD, he is knowledgeable and passionate about research. He is devoted to creating Continuing Medical Education (CME) content that is useful to researchers and practitioners in the medical field. Dr. Howard’s most recent course will walk you through every step of the research project process and earn you CME credit. If you’re interested in the course, click below or visit Obstats.com.